理工学部小森理
教師あり学習と教師なし学習の融合とその肺疾患データ解析への応用
教師あり学習は特徴量xからクラスラベルyを予測する問題として定式化できます。つまり特徴量の空間Xからクラスラベルの空間Yへの写像(判別関数)Fとすると、教師あり学習と教師なし学習
F: X→Y
のように表現できます。yを{0,1}の二値として、xに等分散の正規分布を仮定すると、誤判別確率を最小にするFisherの線形判別関数F(x)が導出されます。また近年注目されている深層学習特にCNNと呼ばれる手法も、尤度から構成される目的関数を最適化する複雑な非線形関数F(x)を推定する問題として定式化できます。
2つ目の教師なし学習とはクラスラベルyの情報は用いず、特徴量xのみを用いてその空間の性質を調べる手法です。典型的なものにK個のクラスターを探索するK-meansの手法などがあります。
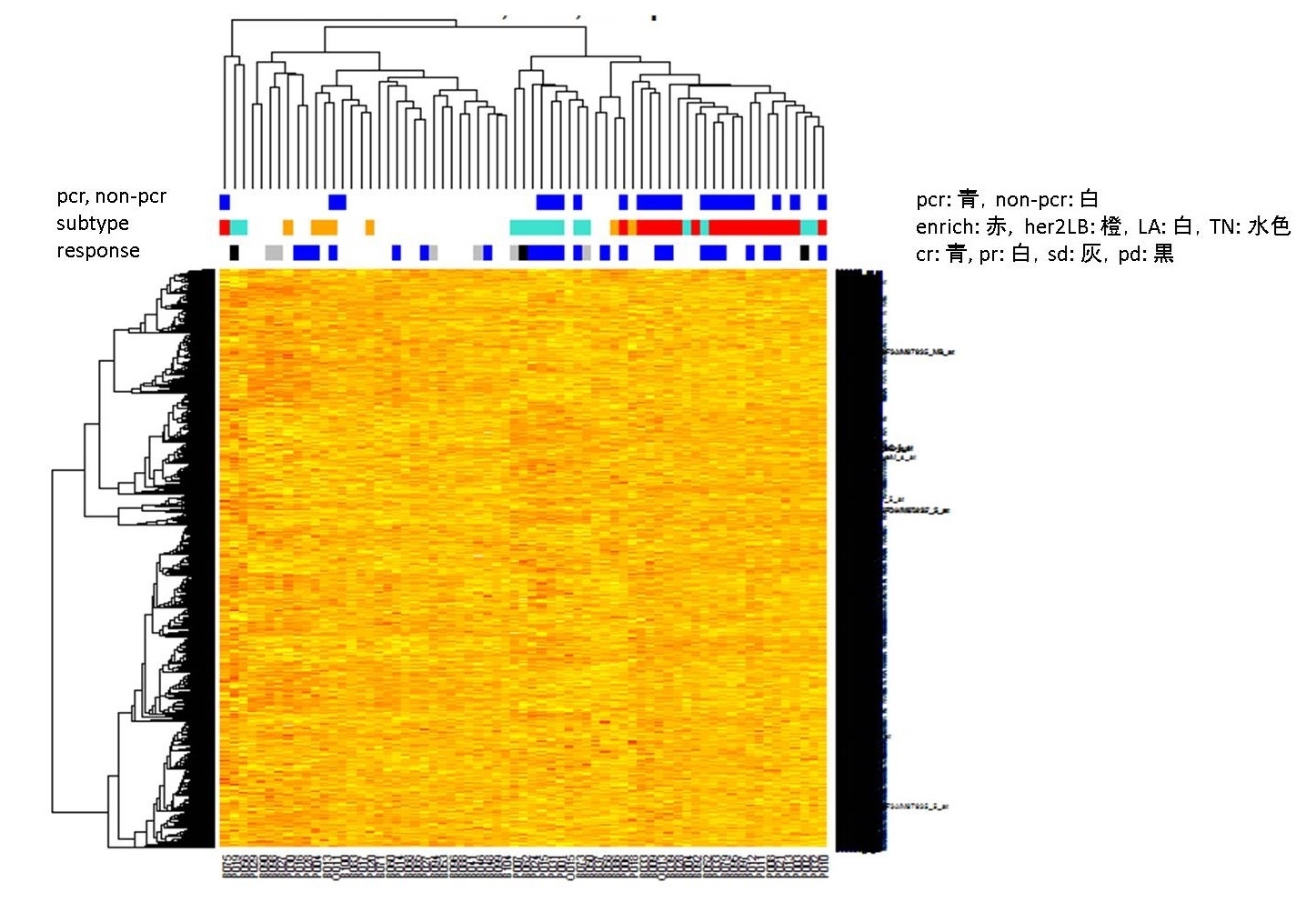
図1の遺伝子発現量のヒートマップの例では縦軸は特徴量x、横軸はクラスラベルyの情報を表しています。このヒートマップから特徴量xのクラスター情報とクラスラベルyの間に密接な関係があることも分かります。このように教師あり学習であるF(x)の推定にも教師なし学習であるクラスターの情報が重要となります。
<図1>
準線形モデルの開発
上記の判別関数F(x)は特徴量xとクラスラベルyの関係性を表しているものと解釈できます。その意味でFisherの線形判別関数はxの各要素が線形に関係しクラスラベルyを定めているというとてもシンプルな構造をモデル化しています。一方で深層学習のような複雑なモデルでは特徴量xとクラスラベルyの関係性の解釈も困難となります。そこで筆者らは各クラスターごとにはシンプルな線形性を仮定し、そのクラスターをKolmogorov-Nagumo平均を使って組み合わせることにより、特徴量xとクラスラベルyとの関係性をより柔軟にモデル化する新たな準線形モデルを提案しました。つまり全体としては複雑な非線形構造を仮定していますが、局所的にはシンプルな線形性を仮定したモデルとなります。
肺疾患データ解析への応用
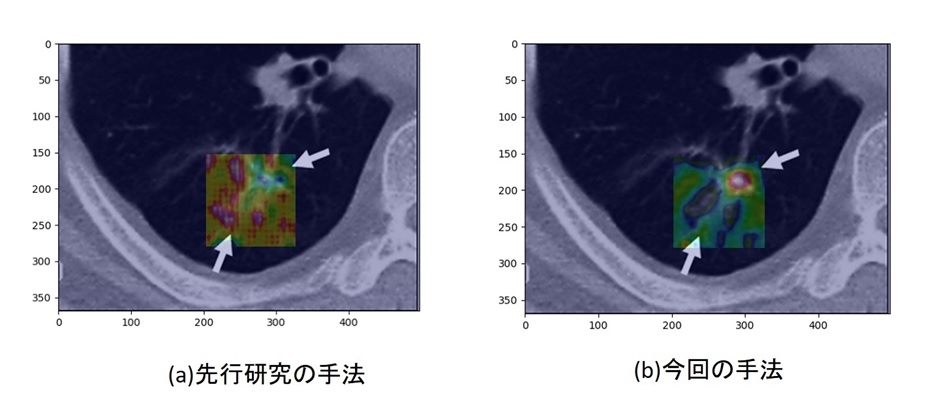
上記の準線形モデリングの考えを肺疾患データ解析に応用する試みも行いました.肺疾患の病型yは大きく分けて12病型に分類され、それを肺の画像データxを使って予測する試みとなります。図2の写真はその1つの病型を持つ画像データに深層学習法であるCNNを適用した結果となります。肺疾患のどの部位が病型に密接に関連しているかを可視化しており、従来法と比較して関連部位の同定がより明確になりました。また判別精度においても改善することができました。
<図2>
Profile

理工学部
小森理
- 専門分野 機械学習、医療統計、生物統計、情報幾何学、データサイエンス
- 担当授業 確率統計、確率論、データ解析法、複雑系解析


